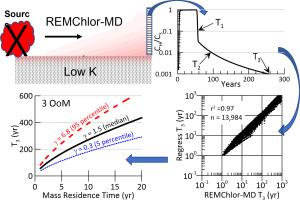
来自低渗透率 (K) 区域的地下水污染物的反向扩散可能是控制下坡监测井达到清理目标时间的主要因素。我们确定了对完全源清除后污染物浓度下降 1、2 和 3 个数量级(T 1、T 2和 T 3 )的时间 (T OoM )影响最大的含水层和污染物特征)。评估了两种含水层配置: (a) 具有有限厚度低 K 层的分层几何 (LG);(b) 具有厚半无限低 K 边界的边界几何 (BG)。半解析建模方法(Muskus 和 Falta,2018 年)用于模拟一系列条件下源移除后的浓度下降,并生成约 21,000 个 T 1、T 2和 T 3的独立值。线性回归用于解释这个大型数据集并建立简单的关系来估计 T OoM从三个特征参数 - 质量停留时间 (T M )、扩散时间 (T D ) 和低 K 与高 K 质量存储的比率 (γ )。TM _是两种几何形状的 T 1、T 2和 T 3最重要的预测因子,并且等于加载期结束时 (T L ) 时的总高和低 K 污染物质量除以质量通量。对于 LG,T 3受 T D = R L L D 2 /(4D*) 的强烈影响,其中 R L是低 K 延迟因子,L D是嵌入的低 K 层的半厚度,D*是有效扩散系数。对于 BG,T 3受 γ 的强烈影响。当 λ L T时,低 K 区的污染物衰减可以显着减少清理时间D > 0.01,其中 λ L是低 K 区的有效一阶衰减率。等于 T M /T D的第一 Damköhler (Da)提供了一个有用的指标,表明反向扩散对 T OoM的相对重要性。当 0.01 > Da > 0.1 时,反向扩散对 T 3的影响最大,然后随着 Da 的增加而减小。反向扩散对T 2的影响较小,对T 1的影响有限。结果总结在一个简单的概念模型中,以帮助评估反向扩散对浓度下降 1-3 OoM 时间的影响。
 "点击查看英文标题和摘要"
"点击查看英文标题和摘要"
Evaluating the impact of back diffusion on groundwater cleanup time
Back diffusion of groundwater contaminants from low permeability (K) zones can be a major factor controlling the time to reach cleanup goals in downgradient monitor wells. We identify the aquifer and contaminant characteristics that have the greatest influence on the time (TOoM) after complete source removal for contaminant concentrations to decline by 1, 2 and 3 Orders-of-Magnitude (T1, T2 and T3). Two aquifer configurations are evaluated: (a) layered geometry (LG) with finite thickness low K layers; and (b) boundary geometry (BG) with thick semi-infinite low K boundaries. A semi-analytical modeling approach (Muskus and Falta, 2018) is used to simulate the concentration decline following source removal for a range of conditions and generate ≈21,000 independent values of T1, T2 and T3. Linear regression is applied to interpret this large dataset and develop simple relationships to estimate TOoM from three characteristic parameters – the mass residence time (TM), diffusion time (TD), and ratio of low K to high K mass storage (γ). TM is most important predictor of T1, T2 and T3 for both geometries and is equal to the combined high and low K contaminant mass divided by the mass flux, at the end of the loading period (TL). For LG, T3 is strongly influenced by TD = RLLD2/(4D*), where RL is the low K retardation factor, LD is the half-thickness of the embedded low K layers, and D* is the effective diffusion coefficient. For BG, T3 is strongly influenced by γ. Contaminant decay in low K zones can significantly reduce cleanup times when λLTD > 0.01, where λL is the effective first order decay rate in the low K zone. The 1st Damköhler (Da), equal to TM/TD, provides a useful indicator of the relative importance of back diffusion on TOoM. Back diffusion impacts are greatest on T3 when 0.01 > Da > 0.1, then decrease with increasing Da. Back diffusion has less impacts on T2, with limited influence on T1. The results are summarized in a simple conceptual model to aid in evaluating the impact of back diffusion on the time for concentrations to decline by 1–3 OoM.































 京公网安备 11010802027423号
京公网安备 11010802027423号