当前位置:
X-MOL 学术
›
Soft Matter
›
论文详情
Our official English website, www.x-mol.net, welcomes your
feedback! (Note: you will need to create a separate account there.)
Plateau–Rayleigh instability in a soft viscoelastic material
Soft Matter ( IF 2.9 ) Pub Date : 2021-3-22 , DOI: 10.1039/d1sm00019e
S. I. Tamim 1, 2, 3, 4 , J. B. Bostwick 1, 2, 3, 4
Soft Matter ( IF 2.9 ) Pub Date : 2021-3-22 , DOI: 10.1039/d1sm00019e
S. I. Tamim 1, 2, 3, 4 , J. B. Bostwick 1, 2, 3, 4
Affiliation
|
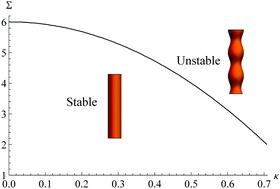
A soft cylindrical interface endowed with surface tension can be unstable to wavy undulations. This is known as the Plateau–Rayleigh instability (PRI) and for solids the instability is governed by the competition between elasticity and capillarity. A dynamic stability analysis is performed for the cases of a soft (i) cylinder and (ii) cylindrical cavity assuming the material is viscoelastic with power-law rheology. The governing equations are made time-independent through the Laplace transform from which a solution is constructed using displacement potentials. The dispersion relationships are then derived, which depend upon the dimensionless elastocapillary number, solid Deborah number, and compressibility number, and the static stability limit, critical disturbance, and maximum growth rate are computed. This dynamic analysis recovers previous literature results in the appropriate limits. Elasticity stabilizes and compressibility destabilizes the PRI. For an incompressible material, viscoelasticity does not affect stability but does decrease the growth rate and shift the critical wavenumber to lower values. The critical wavenumber shows a more complex dependence upon compressibility for the cylinder but exhibits a predictable trend for the cylindrical cavity.
中文翻译:

软黏弹性材料中的高原-瑞利不稳定性
赋予表面张力的柔软的圆柱形界面可能对波浪状起伏不稳定。这被称为高原-瑞利不稳定性(PRI),对于固体,不稳定性由弹性和毛细作用之间的竞争控制。假设材料是粘弹性且具有幂律流变学,则对软的(i)圆柱体和(ii)圆柱腔体进行动力稳定性分析。通过拉普拉斯(Laplace)变换使控制方程与时间无关,该拉普拉斯变换利用位移电势构造了一个解。然后得出色散关系,其取决于无量纲的弹性毛细管数,固体Deborah数和可压缩性数,并计算出静态稳定性极限,临界扰动和最大增长率。这种动态分析可以在适当的范围内恢复以前的文献结果。弹性稳定,而可压缩性则使PRI不稳定。对于不可压缩的材料,粘弹性不会影响稳定性,但会降低增长率,并将临界波数移至较低值。临界波数显示了对圆柱体可压缩性的更复杂的依赖性,但对圆柱腔显示了可预测的趋势。
更新日期:2021-03-22
中文翻译:

软黏弹性材料中的高原-瑞利不稳定性
赋予表面张力的柔软的圆柱形界面可能对波浪状起伏不稳定。这被称为高原-瑞利不稳定性(PRI),对于固体,不稳定性由弹性和毛细作用之间的竞争控制。假设材料是粘弹性且具有幂律流变学,则对软的(i)圆柱体和(ii)圆柱腔体进行动力稳定性分析。通过拉普拉斯(Laplace)变换使控制方程与时间无关,该拉普拉斯变换利用位移电势构造了一个解。然后得出色散关系,其取决于无量纲的弹性毛细管数,固体Deborah数和可压缩性数,并计算出静态稳定性极限,临界扰动和最大增长率。这种动态分析可以在适当的范围内恢复以前的文献结果。弹性稳定,而可压缩性则使PRI不稳定。对于不可压缩的材料,粘弹性不会影响稳定性,但会降低增长率,并将临界波数移至较低值。临界波数显示了对圆柱体可压缩性的更复杂的依赖性,但对圆柱腔显示了可预测的趋势。








































 京公网安备 11010802027423号
京公网安备 11010802027423号