Linear Viscoelasticity of Associative Polymers: Sticky Rouse Model and the Role of Bridges,Macromolecules

当前位置： X-MOL 学术 › Macromolecules › 论文详情

Our official English website, www.x-mol.net, welcomes your feedback! (Note: you will need to create a separate account there.)

Linear Viscoelasticity of Associative Polymers: Sticky Rouse Model and the Role of Bridges
Macromolecules ( IF 5.1 ) Pub Date : 2020-04-20 , DOI: 10.1021/acs.macromol.0c00312
Nuofei Jiang ₁ , Hongdong Zhang ₁ , Ping Tang ₁ , Yuliang Yang ₁

Affiliation

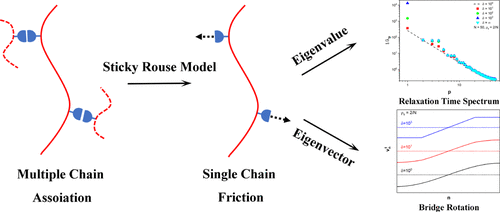
Polymers bearing associative groups can exhibit fascinating rheological behaviors. A modified version of the Rouse model, which is originally used in block copolymers and called the sticky Rouse model here, is proposed to describe the linear viscoelasticity (LVE) of this kind of polymers without the effect of entanglement. By replacing the lifetime of a transient bond by the effective friction on stickers, the calculation of LVE functions is turned into the eigenvalue problem of the sticky Rouse–Zimm (RZ) matrix. The results show that only two parameters, sticker concentration representing the network microstructure and association interaction strength, can understand the LVE for associative polymers. In particular, the description of LVE from previous theories can be integrated in this unified theoretical framework. From the analysis of eigenvectors, it is further inferred that the rotational motion of bridge structures should be responsible for the longest relaxation times in rheology.

中文翻译：

缔合聚合物的线性粘弹性：黏性劳斯模型和桥的作用

带有缔合基团的聚合物可以表现出令人着迷的流变行为。提出了最初用于嵌段共聚物中并在此处称为粘性Rouse模型的Rouse模型的改进版本，以描述这种聚合物的线性粘弹性（LVE），而没有缠结的影响。通过用贴纸上的有效摩擦来代替瞬态键的寿命，LVE函数的计算将转化为粘性Rouse-Zimm（RZ）矩阵的特征值问题。结果表明，只有两个参数，即代表网络微结构的胶粘剂浓度和缔合相互作用强度，可以理解缔合聚合物的LVE。特别是，可以将以前理论中对LVE的描述集成到此统一的理论框架中。

更新日期：2020-04-20

点击分享查看原文

点击收藏

阅读更多本刊新发论文本刊介绍/投稿指南