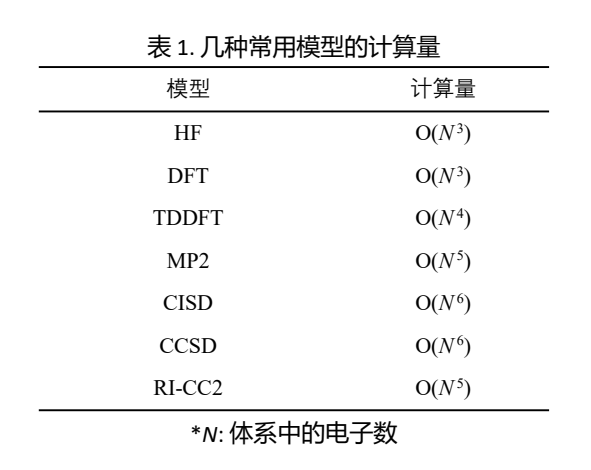
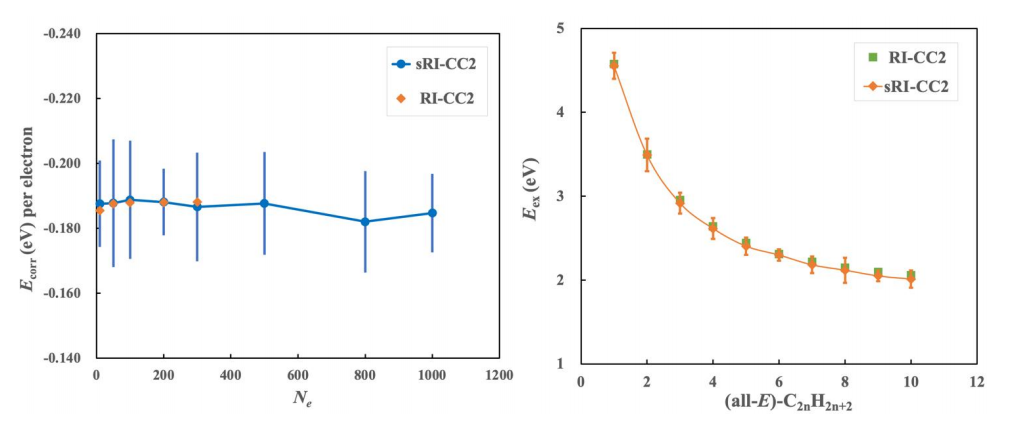
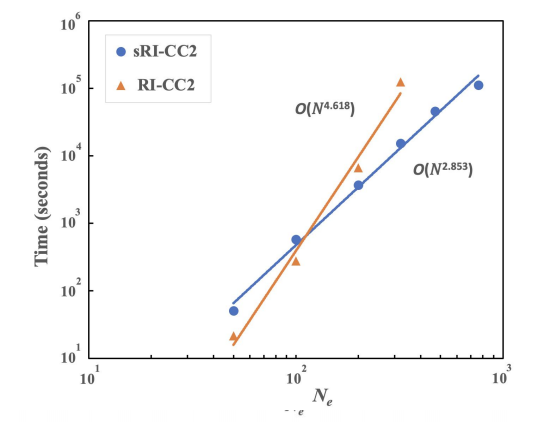
通讯作者：窦文杰 (西湖大学)，Joonho Lee (哈佛大学)

作者： 赵冲霄

在理论化学领域，为复杂体系开发准确且廉价的电子结构计算方法至今仍是一个难题。自上世纪Hartree-Fock方法问世以来，人们为了修正电子关联的部分，发展了一系列的方法，如组态相互作用 (CI), Møller–Plesset微扰理论 (MBPT) 和耦合簇理论 (CC) 等。这些方法为电子结构的分析和计算提供了相对准确的结果，常用的方法如CCSD等极大地推动了相关领域的发展。然而，这些方法通常拥有较高的计算量，因而难以用于复杂大体系的计算。对于动辄成百上千个电子的大分子，现有的方法模型难以满足实际应用的需要。

近日，西湖大学窦文杰教授在JPCA上发表了基于随机轨道恒等式分解的CC2方法 (sRI-CC2) 的研究，与常用的方法相比，可以将计算量由O(N⁵) 显著得降至O(N³)，可用于近千电子大小体系的基态和三重态激发能的计算。

图1. sRI-CC2基态和三重态激发能: (左) 氢二聚体链, sto-3g基组; (右)烯烃链, cc-pVDZ基组

为验证sRI-CC2方法的普适性，作者选取测试不同体系和基组，图1中展示了部分结果。由于用到了随机近似，产生的标准偏差在图中用误差棒体现，随体系增大基本恒定在较小的数值。数据与作为参照的RI-CC2结果基本符合，体现了较高的准确性。

图2. sRI-CC2基态能计算CPU时间 (水分子团簇, cc-pVDZ基组)

图2展示了sRI-CC2方法在计算量上的表现。常用的RI-CC2方法给出了近O(N⁵)的计算量，且由于计算大体系时需要更多的存储，止步于含300电子的水团簇。从近100电子的交叉点开始，新开发的sRI-CC2方法在耗时方面表现更佳，计算量接近O(N³)，能用于近千电子的大体系计算。

综上，窦文杰团队开发的sRI-CC2方法能在基本保证准确性的同时，将计算量显著降低至O(N³)，为大体系的计算有效地提供了一种可替代的方法。团队未来会继续研究大体系低阶计算相关性质和方法，如分析梯度、导数耦合等，并尝试与动力学部分有机结合。

相关论文发表在JPCA上，西湖大学博士研究生赵冲霄为文章的第一作者， 窦文杰教授为通讯作者。

窦文杰。2018年在宾夕法尼亚大学取得化学博士学位，之后在加州大学伯克利分校从事博士后研究。于2021年加入西湖大学开展独立研究工作，组建理论计算化学实验室，现为西湖大学特聘研究员和博士生导师。研究方向主要涉及多体非绝热动力学和大尺度电子结构计算。欢迎对理论计算化学感兴趣的本科生及研究生申请课题组博士研究生，同时课题组诚招博士后和研究助理，实验室提供优厚的个人待遇和有力的职业发展支持。

课题组主页:

https://dougroup.westlake.edu.cn/index.html 

邮箱:

douwenjie@westlake.edu.cn