见微知著——基于大规模分子动力学模拟构建的广义主方程模型成功揭示抗生素抑制细菌基因转录的分子机理

分子动力学模拟是研究蛋白质、酶等生物活性物质全原子精细构象动力学的重要方法，有助于指导药物开发。然而，受限于计算机硬件的计算能力，生物大体系的模拟往往需要消耗大量时间。香港科技大学黄旭辉教授课题组利用广义主方程发展了准马尔科夫态模型算法(quasi-Markov State Models，qMSM)，可广泛应用于大规模生物体系精确动力学计算。通过该模型，黄教授课题组成功揭示了靶向细菌RNA聚合酶的抗生素抑制细菌基因转录的机理，为抗生素的开发提供了可靠的理论指导。该论文近期发表于《美国科学院院报》(Proc. Nat. Acad. Sci. U.S.A.)。

在准马尔科夫模型提出之前，马尔科夫态模型 (Markov State Model, MSM) 被广泛用以研究生物大分子的构象变化。传统的马尔科夫模型通过对时间与空间进行粗粒化处理，在离散的时间序列上建立起离散态之间的动力学。当离散时间序列的间隔（lag time）足够长的条件下，系统的运动仅由当前的状态决定而与之前的历史无关。这种情况被称为马尔科夫过程。在这类马尔科夫过程中，只要得到态与态之间的转移概率，就可以由主方程得到整个系统的长时间演化：

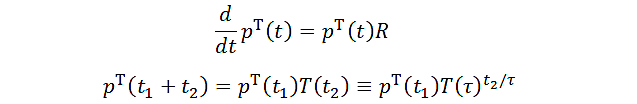
上式中 T(t) 即态与态之间的转移概率 (Transition Probability) 矩阵，R = d lnT(t)/dt为转移速率矩阵 (Transition Rate Matrix)。由此可见，构建转移概率矩阵 T(t) 是构造马尔科夫态模型的核心。根据遍历性公设，一条在相空间中遍历的轨迹采样等同于按概率分布的多条轨迹的采样集合，因此在分子体系中，转移概率矩阵可以通过大量的分子动力学模拟轨迹的数据合集来获取。这样做的好处在于，可以利用不同轨迹采样的相互独立性，使得整个数据集的采样可以在毫不相关的计算设备上同时分别完成，从而通过并行计算显著提高采样效率。

利用传统马尔科夫态模型研究构象变化要求离散时间序列上的动力学没有历史记忆，从而可以由主方程来描述动力学过程。然而，大分子体系的历史记忆可能很长，这就使得主方程所要求的lag time可能过长、甚至远远超出分子动力学模拟单条轨迹的长度，从而对传统马尔科夫态模型提出了相当大的挑战。为了避免花费十倍、百倍的计算资源来获得马尔科夫链，黄教授及其合作者提出准马尔科夫态模型 (quasi-Markov State Models，qMSM)，利用广义主方程来描述分子构象随时间序列的演化。在实践中，广义主方程可以将所需要的轨迹长度缩短5~10倍，因此即使转移矩阵要求的lag time远远超出分子动力学模拟的轨迹长度，广义主方程也可以进行动力学计算。

qMSM 中的广义主方程可以由投影算子理论和 Nakajima-Zwanzig 方程得到，其数学形式为：

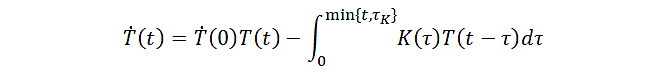
右侧第一项与原始主方程对应，右侧第二项即为动力学体系的历史记忆，其中记忆核 K(τ)随时间快速衰减，并且在τ = τ_K时衰减至可忽略不计。通常情况下，τ_K是远远小于马尔科夫态模型的 lag time 的，因此广义主方程所要求的 MD 轨迹长度是远小于马尔科夫态模型的lag time的。关于基于广义主方程的模型来描述构象动力学的理论在黄教授课题组前期的JCP文章有更详细的阐述 (J. Chem. Phys., 2020, 153, 014105)。

利用准马尔科夫模型，黄教授课题组成功揭示了靶向细菌RNA聚合酶的抗生素抑制基因转录的机理。转录是细菌细胞中至关重要的过程，其中DNA中的遗传信息通过转录产生信使RNA，为翻译执行细胞功能的蛋白质提供基础，因此抑制转录过程能有效威胁细菌的生存。RNA聚合酶是参与细菌转录的核心酶，故很有希望成为新一代抗生素的目标。在转录时，RNA聚合酶需要通过DNA熔解来启动转录过程，即聚合酶加载DNA，并将双链DNA分离为单链DNA，才能读取遗传信息。这是一个多步骤且高度动态的过程，受RNA聚酶中两个类似于蟹爪形状的柔性钳装结构（夹钳和β瓣）作为loading gate进行调控。因此，对DNA熔解以及loading gate运动的研究，将会有利于了解RNA聚合酶如何调控细菌基因转录，从而促进新一代以聚合酶为靶标的抗生素的研究和发展。

黄教授课题组通过研究loading gate开放与关闭的动力学过程，揭示了抗生素Myxopyronin抑制聚合酶解旋DNA的机理。他们发现，Clamp底部switch 2区域的折叠态转变对Clamp的打开至关重要。Clamp打开的整个过程需要经历两个部分开启的中间态，而Myxopyronin会结合在其中的一个中间态，从而抑制RNA聚合酶的关闭，并阻止DNA的熔解，对细菌带来致命性的影响，由此成功揭示了Myxopyronin抑制细菌转录的作用机理。

更有趣的是，黄教授课题组发现β瓣在DNA加载到RNA聚合酶内部的过程中扮演着举足轻重的角色。他们发现，β瓣的打开比Clamp的打开慢了四个数量级；并且在不打开钳位的情况下，β瓣的打开在空间上足以容纳双螺旋DNA。这一发现突显了β瓣的重要性，为作用于β瓣以停止转录的抗生素开发提供了新的可能。

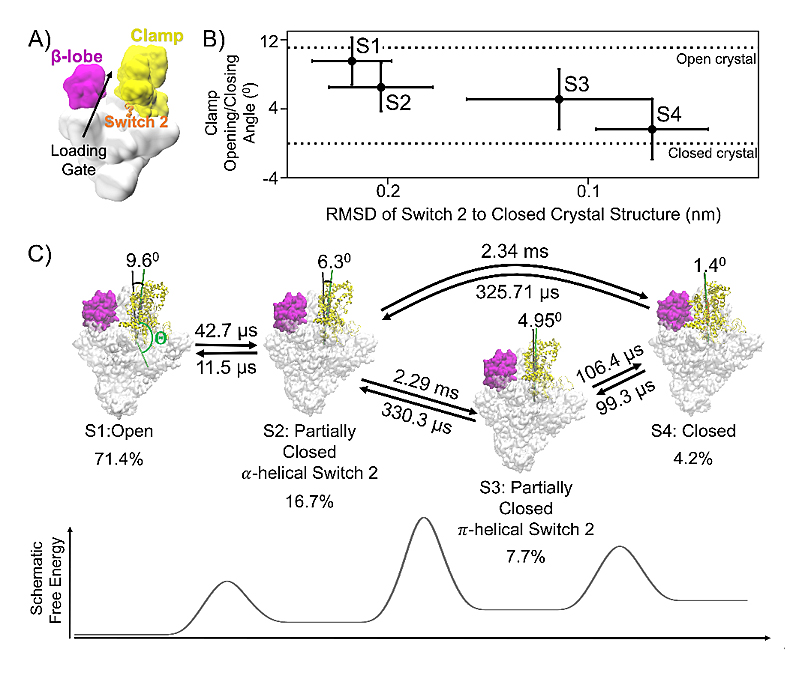
图1. 通过qMSM确定RNAP的钳制结构从开启到关闭构象需要历经四个亚稳态。A） 细菌RNA聚合酶结构。clamp, β-瓣和switch region 2分别显示为黄色、品红和橙色。B） qMSM确定的四个亚稳态构象展现了switch region 2的钳位的不同开闭程度。C）四个亚稳态之间的动力学转化以及qMSM计算的平均转换时间。

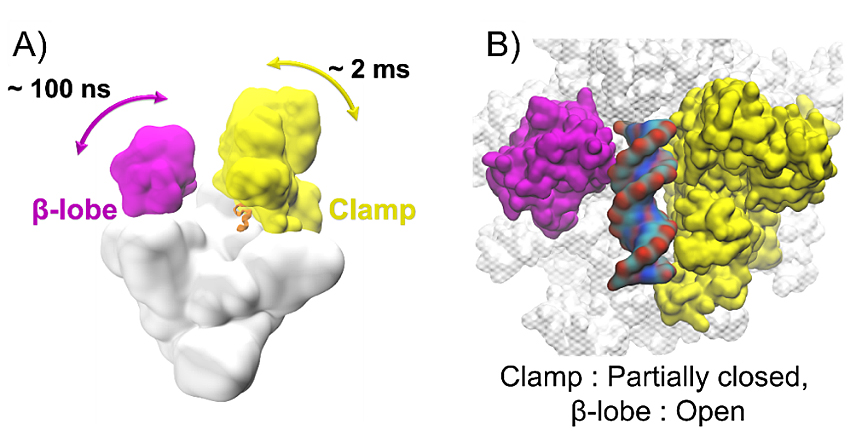
图2. (A) 细菌RNA聚合酶随时间的示意图β-瓣（洋红色）和clamp（黄色）打开和关闭。(B) 聚合酶中双链DNA的模型，其中β-瓣是开放的，clamp是部分闭合的。

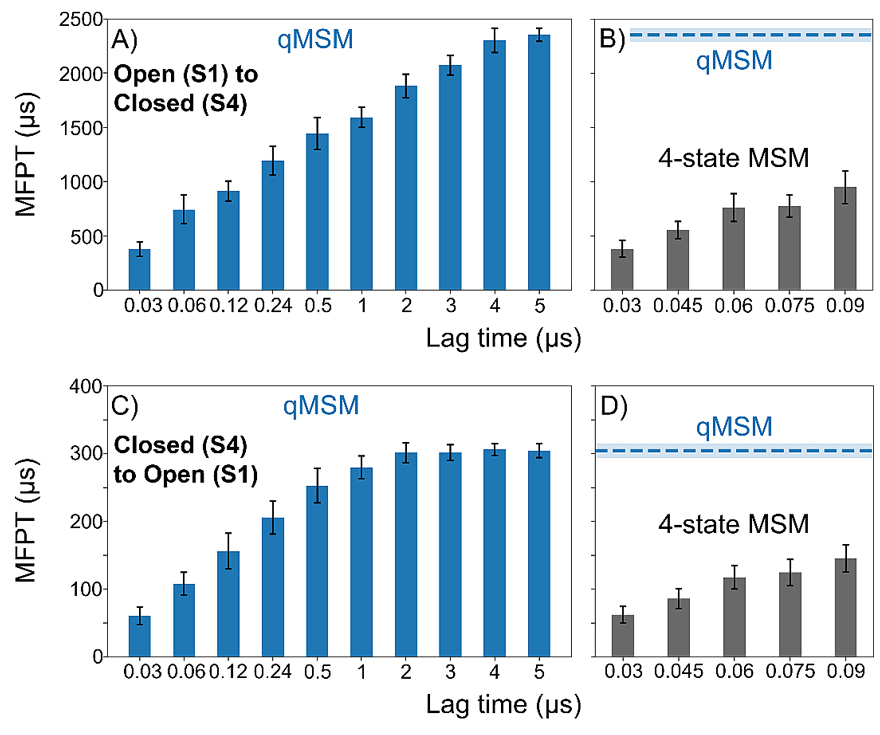
图3. 构象亚稳态S1和S4相互转变的Mean First Passage Time (MFPT)。(A-B) 是S1到S4的MFPT，(C-D)是S4到S1的MFPT。其中(A,C)的MFPT和(C,D)中的虚线由qMSM在不同lag time下得到的等效TPM计算得到，(B,D)则直接由4态的马尔科夫态模型得到。其中 (B,D)中的虚线是 lag time为5 µs时的计算结果。

同时，黄教授课题组发现，在计算RNA聚合酶的构象转变动力学模型时，基于广义主方程的qMSM可以得到比MSM更好的结果。如图3(A,C)所示，如果要准确计算整个loading gate的开放(亚稳态S4->亚稳态S1)与关闭(S1->S4)过程所需的时间，则必须要构造lag time长达5 µs的MSM才能得到正确的结果。而这一时间长度远远超过了单条MD轨迹的长度，因此用传统的MSM是不可能实现的。图3(B,D)显示，根据MD轨迹直接构造MSM进行计算(柱状图)所得的MFPT将远远快于qMSM的结果(虚线)。由此可见，qMSM对长时间构象动力学模拟的准确性远远胜过MSM (如预测图3中RNA聚合酶loading gate打开或者关闭所需的时间)。

该工作将基于广义主方程发展的准马尔科夫模型应用于近55万原子的生物大体系进行动力学计算，并且成功预测了RNA聚合酶柔性钳子的微秒尺度的动力学，为大体系动力学的准确计算提供了新思路。该工作的第一作者是香港科技大学的Ilona Unarta博士，通讯作者为香港科技大学的黄旭辉教授，其他合作者来自京都大学和阿卜杜拉国王科技大学。

原文（扫描或长按二维码，识别后直达原文页面，或点此查看原文）：

Role of Bacterial RNA Polymerase Gate Opening Dynamics in DNA Loading and Antibiotics Inhibition Elucidated by quasi-Markov State Model

Ilona Christy Unarta, Siqin Cao, Shintaroh Kubo, Wei Wang, Peter Pak-Hang Cheung, Xin Gao, Shoji Takada, and Xuhui Huang

Proc. Nat. Acad. Sci. U.S.A., 2021, 118, e2024324118, DOI: 10.1073/pnas.2024324118