反萤石Cu2S系列拓扑材料中的正负自旋轨道耦合、左右自旋手征、Nodal box和杂化表面态

自旋轨道耦合（spin-orbit coupling，SOC）是一个非常重要的概念，在材料的电子结构中扮演着极其重要的性质。那么什么是SOC呢？直观地说，就是电子在绕原子核转动的时候，站在电子的角度看，它感受到的电场一直在发生变化，变化的电场产生磁场，磁场与电子的自旋相互作用，这就是SOC。取球对称近似，SOC可以写成λl•s的形式，其中l 是轨道角动量，s 是自旋角动量，λ 是相互作用强度。

什么是负SOC？SOC的符号又是怎么回事呢？首先说一下通常的SOC，也就是正SOC。以p轨道为例，p轨道有p_x、p_y和p_z三个轨道，假设晶体场环境对它们的影响一样，不考虑SOC时，这三个态构成的能带在Γ点一般是简并的。考虑SOC后，能带劈裂为两组，一组是j = 1/2的二重态，一组是j = 3/2的四重态，前者比后者的能量低，这就是正SOC的情况。当j = 1/2的能量高于j = 3/2的能量时，这时SOC引起的能级分裂次序是相反的，科学家们就把这种SOC称之为负SOC。

据介绍，负SOC早在几十年前就被科学家们在ZnO材料中发现了，只是由于负SOC对ZnO的电子结构的影响远低于材料的化学势，其作用不太明显，因此鲜为人知。直到近几年在拓扑绝缘体和拓扑半金属的研究中，科学家们才注意到负SOC的重要性。据他们介绍，负SOC来源于d轨道的t_2g(d_xy,d_yz,d_xz) 成份，其有效SOC是负的。在正八面体或正四面体晶体场中，d轨道劈裂为两组，一组是t_2g(d_xy,d_yz,d_xz)，另一组是e_g(d_x2-y2,d_z2)，这种劈裂是由对称性决定的。把t_2g(d_xy,d_yz,d_xz)单拿出来，其有效角动量为1，与p轨道类似，考虑SOC后与p轨道有相似的劈裂方式，唯一的差别是系数多了一个负号，其后果是j = 1/2的态高于j = 3/2的态（如图1所示）。在实际材料中，会发生p-d轨道杂化：如果p轨道占主导，SOC就是正的；如果t_2g(d_xy,d_yz,d_xz) 轨道占主导，SOC就是负的。

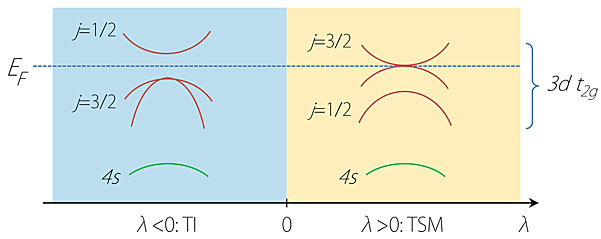
图1. p轨道的SOC是正的，如黄色区域所示；d-t_2g的SOC是负的，如蓝色区域所示。图片来源：J. Phys. Chem. Lett.

这样以来，如果我们能够找到一类材料，调节其SOC的符号，就可以实现体系从拓扑半金属到拓扑绝缘体的拓扑相变。既然负SOC如此奇妙，存在这样的候选材料吗？尽管这样的材料的确很少，但仍然是存在的。由北京航空航天大学、中科院物理所和新加坡科技设计大学组成的联合研究团队发现，反萤石结构的Cu₂S系列材料就具有这样的属性：Cu₂S是负SOC拓扑绝缘体，Cu₂Se是正SOC的拓扑半金属，破缺空间反演对称性的CuAgSe是Nodal box拓扑半金属，单向拉伸的CuAgSe是Weyl半金属（J. Phys. Chem. Lett., 2017, 8, 3506-3511）。

首先讨论拓扑绝缘体Cu₂S。我们知道HgTe是正SOC的拓扑半金属，要想打开能隙，使之变成真正的拓扑绝缘体，有三种办法：（1）截取薄膜，形成二维量子阱，体系由于量子受限效应打开能隙；（2）单轴压缩，破坏j = 3/2的四重简并态，从而打开能隙；（3）改变SOC的符号，使得j = 1/2的能量高于j = 3/2的能量，电子数就刚好填充在二者之间。这三种方法都可以使HgTe变成拓扑绝缘体，但前两个办法需要破坏体系的晶体对称性，而第三个办法对不需要破坏晶体对称性。Cu₂S材料就是由于第三个原因打开能隙的负SOC拓扑绝缘体，其费米面附近主要是Cu的t_2g轨道贡献的，这时，其表面态也与正SOC拓扑绝缘体有很大不同，狄拉克锥上半部的自旋-动量锁定（spin-momentum locking）是右手螺旋的（如图2所示），而正SOC的情况是左手螺旋的，刚好相反。

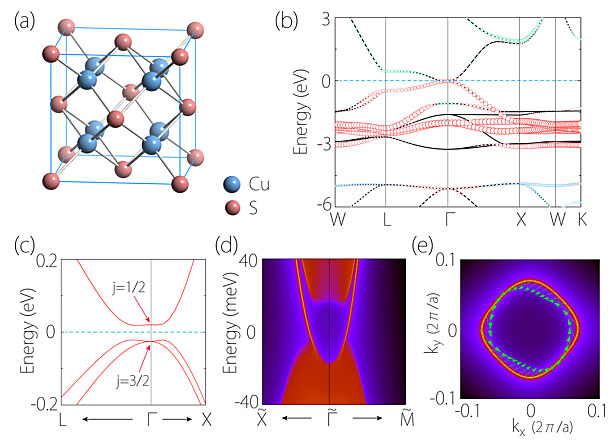
图2. 负SOC材料TlN的表面态与自旋结构，其手性与正SOC的拓扑材料的自旋结构指向相反（如图3中Cu₂Se）。图片来源：J. Phys. Chem. Lett.

接下来讨论拓扑半金属Cu₂Se。把S替换成Se后，一方面Se的p轨道SOC比S的大，另一方面Cu₂Se材料中的p-d杂化也更强，p轨道的SOC就占主导地位，符号为正，体系就是拓扑半金属。表面态形成的狄拉克锥埋在费米面下面，其自旋结构为左手螺旋的，与负SOC的情况相反（图3）。

图3. 正SOC拓扑半金属Cu₂Se，能带、表面态与自旋结构（手性与负SOC相反）。图片来源：J. Phys. Chem. Lett.

最后讨论CuAgSe中的Nodal box和Weyl半金属态。CuAgSe与Cu₂Se相比，破坏了空间反演对称，能带的两重简并解除，在Γ点附近的能带有一些起伏，从而形成了一些能带交叉。取一个镜像面，这些能带交叉点连线成蝴蝶型；在整个第一布里渊区，这些能带交叉点形成Nodal box型，如图4所示。尽管这是考虑SOC后的结论，这里的Nodal line不需要非简单（nonsymmorphic）对称性的保护，这也是这篇文章的一个新颖点。

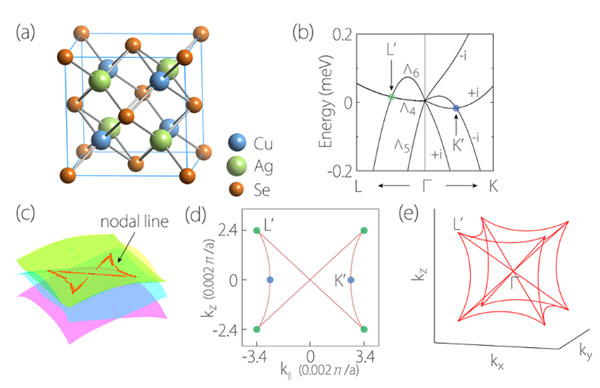
图4. CuAgSe材料的（a）晶体结构，（b）Γ点附近的能带，导带和价带在（c）[110]镜像面上的交叉点，（d）形成蝴蝶型，（e）在整个第一布里渊区形成Nodal box型。图片来源：J. Phys. Chem. Lett.

有趣的是，如果把CuAgSe单向拉伸，Nodal box解除，但形成了Weyl半金属态，Weyl点的分布和费米弧，如图5所示。需要说明的是，关于在这类材料中形成Weyl半金属的情形，南京大学的张海军教授团队有两篇文章对此做了详细的介绍，他们研究的是HgTe材料和黄铜矿材料（Nat. Commun., 2016, 7, 11136; Phys. Rev. Lett., 2016, 116, 226801）。尽管材料不同，Weyl点的形成机制是一样的。

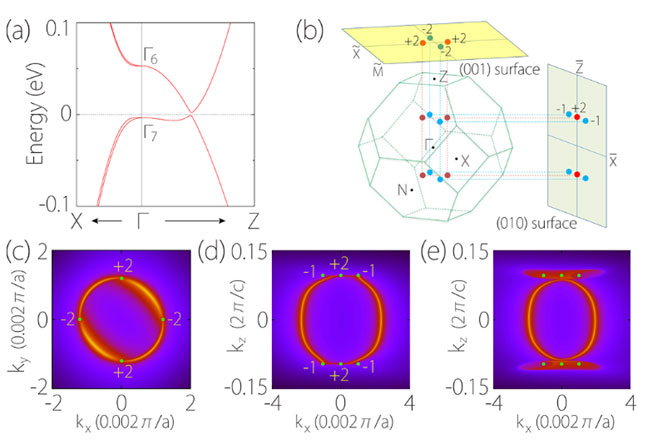
图5. CuAgSe受到3%的单向拉伸：（a）Γ点附近能带，在Γ-Z沿线上有能隙打开；（b）Weyl点在第一布里渊区的分布；（c）［001］表面的费米弧；（d）［010］表面的费米弧和表面态，（e）［010］表面在-5meV处的等能面，费米弧和杂化表面态区分的更清晰。图片来源：J. Phys. Chem. Lett.

除此之外，还有一类Wurzite结构的TlN系列材料也具有上述特性（Phys. Rev. B, 2014, 90, 245308）。TlN是负SOC的拓扑半金属，TlAs是正SOC的狄拉克半金属，TlP基本位于二者的分界线上。值得注意的是，在这类材料的拓扑相变中，晶体的对称性无需改变，这不同于朗道的相变理论，属于拓扑相变。

上述两篇文章主要是北京航空航天大学的胜献雷博士先后在中科院物理所（合作导师：翁红明、方忠、戴希）和新加坡科技设计大学（合作导师：杨声远）做博士后期间的完成的。感兴趣的读者可以进一步阅读原文，两篇文章通过对两类不同材料的研究，对SOC符号变化引起的拓扑物态给予了系统的讨论，内容互有补充。

1. 该论文作者为：X.-L. Sheng, Z.-M. Yu, R.Yu, H. Weng, and S. A. Yang

原文（扫描或长按二维码，识别后直达原文页面，或点此查看原文）：

d Orbital Topological Insulator and Semimetal in the Antifluorite Cu₂S Family: Contrasting Spin Helicities, Nodal Box, and Hybrid Surface States

J. Phys. Chem. Lett., 2017, 8, 3506-3511, DOI: 10.1021/acs.jpclett.7b01390

2. 该论文作者为： X.-L. Sheng, Z. Wang, R.Yu, H. Weng, Z. Fang, and X. Dai

原文（扫描或长按二维码，识别后直达原文页面，或点此查看原文）：

Topological insulator to Dirac semimetal transition driven by sign change of spin-orbit coupling in thallium nitride

Phys. Rev. B, 2014, 90, 245308, DOI:https://doi.org/10.1103/PhysRevB.90.245308

官网报道

http://datastorage.buaa.edu.cn/info/1043/1370.htm